Distance function ray marching in WebGL
Using distance functions and ray marching to render scenes is nothing new, but I wanted to try it myself. Most of the demos at shadertoy.com use this technique, and I've always been impressed by how such beautifully rendered scenes can be made using at most a few hundred lines of GLSL.
In these types of renderers, the only geometry loaded into the GPU is a single plane between the points (-1, -1, 0) and (1, 1, 0). All the vertex shader has to do is pass these X & Y coordinates through unmodified to gl_Position and the plane will cover the screen:
attribute vec3 position;
varying vec2 uv;
void main() {
gl_Position = vec4(position, 1.0);
uv = position.xy;
}
Code for setting up a canvas, getting the WebGL context, loading the polygon and other data, and linking programs can be found in my sandbox project.
Fragment Shader Basics
The real magic in ray marching happens in the fragment shader, where the GPU basically asks what colour (gl_FragColor) each pixel (gl_FragCoord) of a rendered surface should be. A really basic shader might look like this:
precision mediump float;
void main() {
gl_FragColor = vec4(
smoothstep(-1.0, 1.0, sin(gl_FragCoord.x / 5.0)),
smoothstep(-1.0, 1.0, sin(gl_FragCoord.y / 10.0)),
1.0, 1.0
);
}
This should make some intuitive sense. What we're outputting is a 4 component vector (RGBA) expecting values in the range [0, 1], and the red and green channels vary based on the screen pixel coordinates. The smoothstep function just maps the [-1, 1] bounds of a sine wave to [0, 1].
By adding in some uniforms whose values are bound to the program by JavaScript each frame, we can give the shader more information like the size of the canvas and the time since its creation:
precision mediump float;
uniform vec2 canvasSize;
uniform float timeSec;
void main() {
gl_FragColor = vec4(
smoothstep(-1.0, 1.0, gl_FragCoord.xy / canvasSize.xy),
smoothstep(-1.0, 1.0, sin(timeSec)),
1.0
);
}
Ray Casting & Marching
Now that we can render a different colour for each pixel of the screen, we can draw a 3D scene on the 2D surface using a more complex fragment shader.
The idea is to pick some arbitrary point in space as the camera origin, then pretend that the 2D surface we're drawing with the fragment shader is sitting right in front of that camera defining its field of view. For each pixel of the surface, a ray is cast out from the camera and passing through that pixel into the scene. The colour of that pixel is the colour of the scene at the end of (or accumulatd along) that ray:
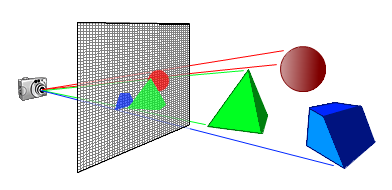
All this logic will be written in the shader, including the description of the scene. To know if the ray missed or hit the objects in the scene, we can use the ray marching technique. This requires having a function that for any arbitrary point in space returns the distance to the nearest surface. For example, the distance from any point to a sphere centered at the origin is:
float sphereDistance(vec3 point, float radius) {
return max(0.0, length(point) - radius);
}
To find out where the ray hits the sphere, the ray is advanced forwards in steps. After each step, we check how far away the sphere is from the leading point of the ray. If the distance is below some threshold EPSILON, then it's considered a "hit". Otherwise, the ray steps forward until we decide to give up after MAX_STEPS or the ray has travelled over MAX_DISTANCE. If the step size is too large we risk going through the sphere, but if it's too small then the algorithm will be too expensive. If the distance to the sphere surface after each step is used as the next step distance, then the ray is guaranteed never to step through the surface.
float march(vec3 rayOrigin, vec3 rayDirection) {
float rayLength = 0.0;
for (int i = 0; i < MAX_STEPS; i++) {
vec3 leadingPoint = rayOrigin + rayLength * rayDirection;
float distanceToScene = sphereDistance(leadingPoint, 2.0);
rayLength += distanceToScene;
if (distanceToScene < EPSILON) return rayLength;
if (rayLength > MAX_DISTANCE) break;
}
return -1.0;
}
Visually, the algorithm looks like this:
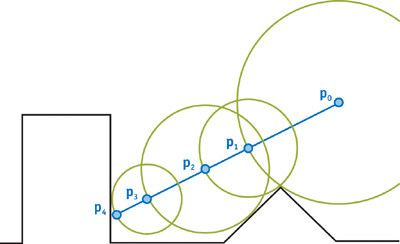
All together:
precision mediump float;
const float EPSILON = 0.001;
const float MAX_DISTANCE = 75.0;
const int MAX_STEPS = 256;
uniform vec2 canvasSize;
uniform float timeSec;
vec3 repeat(vec3 point, vec3 c) {
return mod(point, c) - 0.5 * c;
}
float sceneDistance(vec3 point, float radius) {
return max(0.0, length(repeat(point, vec3(6.0))) - radius);
}
float march(vec3 rayOrigin, vec3 rayDirection) {
float rayLength = 0.0;
for (int i = 0; i < MAX_STEPS; i++) {
vec3 leadingPoint = rayOrigin + rayLength * rayDirection;
float distanceToScene = sceneDistance(leadingPoint, 2.0);
rayLength += distanceToScene;
if (distanceToScene < EPSILON) return rayLength;
if (rayLength > MAX_DISTANCE) break;
}
return -1.0;
}
vec3 circlePath(float y, float radius, float time) {
return vec3(sin(time) * radius, y, cos(time) * radius);
}
void main() {
//camera setup
vec3 cameraPos = circlePath(0.5, 5.0, timeSec / 2.0);
vec3 cameraLookAtPos = vec3(0.0);
vec3 cameraUpDir = vec3(0.0, 1.0, 0.0);
vec3 cameraLookDir = normalize(cameraLookAtPos - cameraPos);
//screen setup
vec2 screenCoord = gl_FragCoord.xy / canvasSize.xy - 0.5;
vec3 screenXDir = normalize(cross(cameraUpDir, cameraLookDir));
vec3 screenYDir = cross(cameraLookDir, screenXDir);
vec3 screenOrigin = cameraPos + cameraLookDir;
//ray setup
vec3 rayOrigin = screenOrigin +
screenCoord.x * screenXDir * canvasSize.x / canvasSize.y +
screenCoord.y * screenYDir;
vec3 rayDir = normalize(rayOrigin - cameraPos);
float rayLength = march(rayOrigin, rayDir);
gl_FragColor = rayLength == -1.0 ?
vec4(0.0) : //miss (transparent)
vec4(vec3(1.0 - rayLength / 50.0), 1.0); //hit
}
Further Effects
Iñigo Quílez's documentation has been an invalable resource for me. In particular:
Here's a demo incorporating reflections, ambient occlusion, soft shadows, surface shading, animation, and post processing:
Happy shading :)